Rich Tasks
Rich Tasks: What is it?
- A task that explicitly requires students to make sense of mathematics and to make connections between concepts, procedures, problem situations, representations and tools.
- Can be an open-ended problem, with a variety of possible solution paths that range from simple to complex.
- Can require justification, where students have to provide reasoning and evaluate the reasoning of others.
- Can include incomplete information, and provide a variety of access points to different students
West (2002)
Rich Tasks depend on many factors...
- Is a task that requires students to move beyond what they already know. What may be rich for a kindergartner is not a rich task for a fifth grader (i.e. If there are 16 people in a room, how many eyes are in the room?)
- Requires a culture of inquiry and persistence.
- Is supported by skillful teaching moves. Alternatively, a rich task can be undermined by teacher moves that remove the demand for student sense-making. (If a teacher tells students what to do too quickly, or does not allow students to make sense of alternative solutions, for instance.)
West (2002)
Why use Rich Tasks:
Maintains academic rigor in your lessons because there are no obvious procedures to follow or “key words” to clue you into what operation to use. Thinking and application of concepts is required.
Builds in differentiation: both proficient and less proficient students can be challenged and can show success because everyone has access and students can journey very far down conceptual paths.
Promotes academic talk between and among students because it provides important ideas to wrap one’s mind around and promotes the capacity to construct a mathematical argument.
Is versatile:Some rich tasks can be used as quick warm up tasks, in independent practice or group work, as a Think-Pair-Share, as a main task or homework task or for assessment.
Is a highly efficient method of assessment of students, either formally or informally and provides ample opportunities for students to represent their mathematical ideas using models and written language.
Builds in differentiation: both proficient and less proficient students can be challenged and can show success because everyone has access and students can journey very far down conceptual paths.
Promotes academic talk between and among students because it provides important ideas to wrap one’s mind around and promotes the capacity to construct a mathematical argument.
Is versatile:Some rich tasks can be used as quick warm up tasks, in independent practice or group work, as a Think-Pair-Share, as a main task or homework task or for assessment.
Is a highly efficient method of assessment of students, either formally or informally and provides ample opportunities for students to represent their mathematical ideas using models and written language.
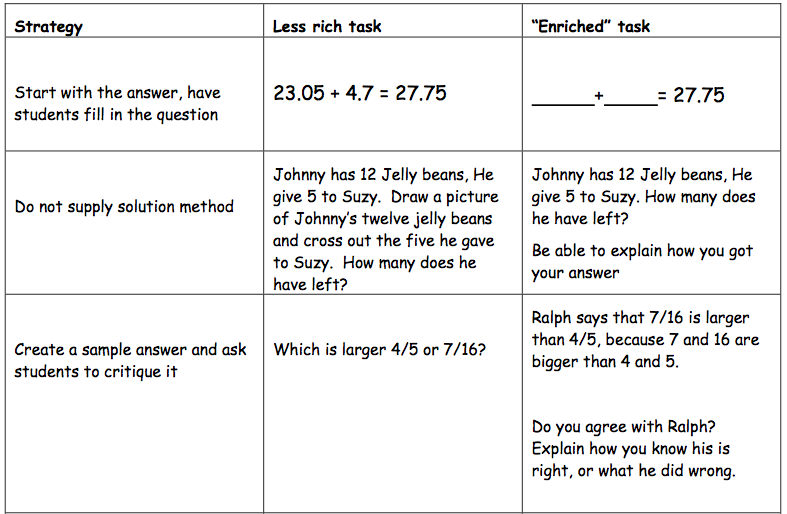
How it looks:
How to construct Rich Tasks or adapt tasks to "Enrich" them: