Gr. 4/5: Minecraft Math: Distinguishing Area and Perimeter
This lesson was developed and used with grade 4 and 5 Home School Program students who were continually failing area and perimeter tests. When asked to design a series of lessons that could help deepen student understanding of area and perimeter, I went back to the curriculum grade expectation that highlights that problems involving area and perimeter be meaningful. In asking students what is meaningful at their stage in life, their response was video games. Although video games are traditionally not included in math instruction, I began to realize that in many of the popular video games incorporated procedural math skills.
Minecraft: About the game:
|
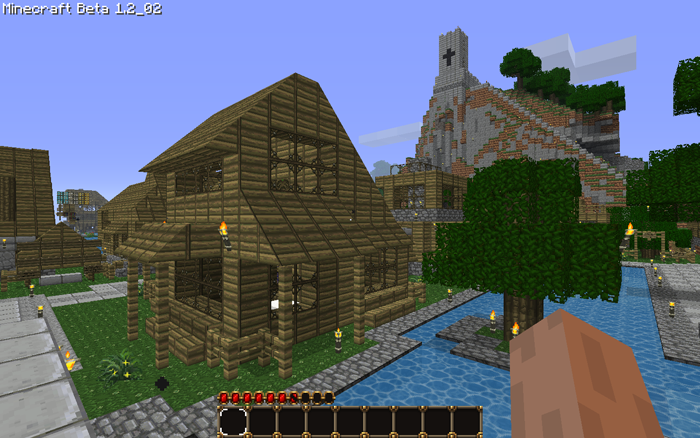
Players create villages and towns out of these cubes that become sustainable communities (they construct mines, farms etc.). (see photo on right)
Understanding the basic concepts of area and perimeter is essential for structure designing. |
One of the basic premises of the game is for players to construct communites that are asthetically appealing and structurally sound. This is done through building with unifix-like blocks. All building materials use identical sized building blocks (see photo on left).
|
|
Grade: 4/5
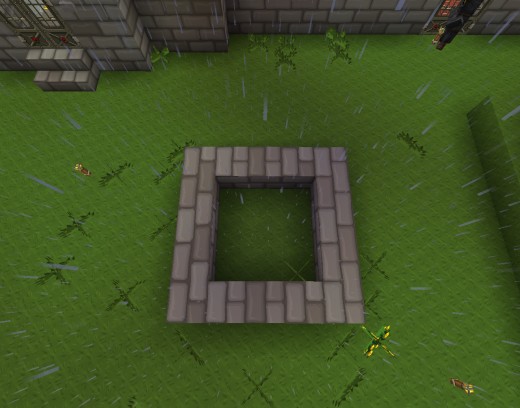
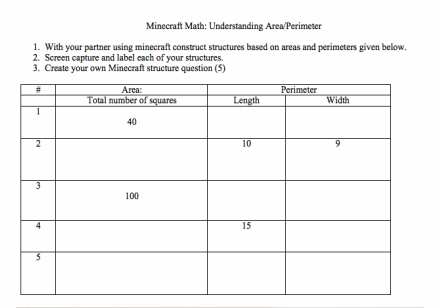
Purpose: Is to pose meaningful problems that encourage students to demonstrate (and use) area and perimeter vocabulary. Student Grouping: Rich Talk: Mini Lesson done with small group Rich Task: partners or individually Questions: Perimeter: 1. If the total perimeter for my house was 40 blocks, what is the length of each side? (see photo below) 2. Is there another way in which you could build a structure with a perimeter of 40 (using only 40 blocks)? Show your work Area: Building Roofs
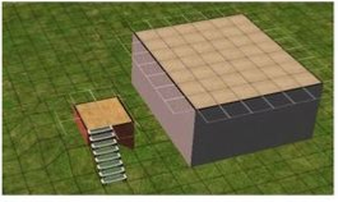
1. How many blocks are needed to construct this roof (the tan blocks) 2. How many blocks are needed for each side? 3. How might we change the structure (shape) of the building but keep the same number of tiles for the roof? What is the difference of the number blocks on each side of the roof? 4. What patterns can you see in relation to total number of blocks and length of each side? Student Questions Example:
Assessment:
Diagnostic: Can students use math language (perimeters and areas) correctly?
Formative: Can they represent their understanding in different ways (be able to construct different structures based on set areas/perimeters? Summative: Students will submit work and photos for assessment. |
Curriculum Expectations:
Materials:
- SMARTBoard (with internet access)
- Computers for pairs of students - Paper, pencils - unifix cubes - Work sheet with questions (as supplimented for students who need it). - File folder on desktop for students to label/file their screen captures. Next Steps:
Have students create their own question (a question 5). Have students attempt to build. Does the perimeters/areas match? If not, how could you change it to work? Is there another way we can change a variable (such as perimeter) but keep area the same? How many ways can we do this?
|