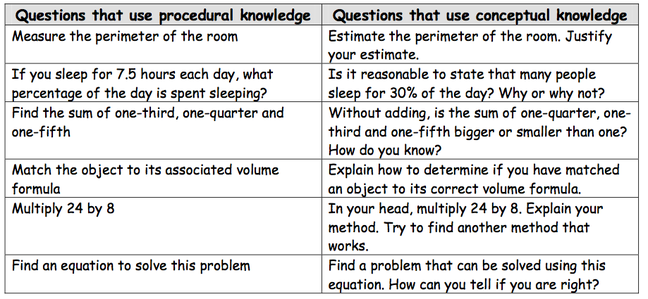
Procedural vs. Conceptual Knowledge
|
|
What they sound like in math instruction:
What the research says:
The debate over whether it is better to teach conceptual or procedural math understanding first has been contested over the past century. Significant research has been done in attempts to
settle this debate and declare one superior over the other (Rittle-Johnson, 1999, Gleman & Williams, 1997, Halford, 1993, Arslan, 2010). In terms of education, this research has greatly impacted teaching and learning approaches to math. In a report done by Barr, Doyle, Clifford, De Leo, Dubeau (2003) they pointed out teachers main complaints about student responses to mathematics (see table).
"...focus needs to be on relationships between conceptual and procedural knowledge in math"
Star (2002) |
Star (2002) argues that instead of debating over superiority, education needs to consider the relationships that exist between these two approaches to math understanding. In Star's perspective, conceptual and procedural knowledge exist on a learning continuum and cannot be separated. With distinct differences between each pole of the continuum the aim of research should be to focus on how the relationships, connections, and intersections between these two approaches impact and deepen student learning.
|
The Learner:
Barr, Doyle et. al. (2003) point out that when we ask students to perform a procedure such as solving an equation, students can often follow an example and get a correct answer without understanding how or why the process works. Traditionally, the majority of assessment in math learning has been based on students' abilities to manipulate knowledge in a procedural format. Tests, exams and quizzes aimed at students producing correct answers highlight their abilities to show how the math processes work, but do not shed light on the deeper meaning of why.
|
In a study done by Star (2002) desgined to highlight children’s understanding of basic algerbra, he found that there were 3 types of students:
In Star’s opinion student C demonstrates both a conceptual and procedural understanding of the problem. They can see math understanding as infinate and complex. Wolfram (2010) argues that math outside of math classrooms involves the following steps:
He points out that too often the majority of math instruction concentrates on stage 3 (Computation) and does not focus on teaching students how to develop math thinking that relates to being able to pose relevant meaningful questions of ideas that exist outside the classroom. |
Student A:
Could demonstrate one method of solving the problem
Student B:
Could demonstrate 1-2 methods of solving the problem
Student C
Could see problem as complex, with many different methods in which to arrive at answer
|
Wolfram notes that in today's global society, careers that use math more often than not rely on computers to do computational tasks (stage 3) and individual creativity and understanding of complexities of math are then responsible for stages 1, 2, and 4.
Delpit (2012) points out that part of the struggle with standardized curriculums (the curriculum that is taught in schools today) is that it does not completely address the individual child: the culture from which they come; the language in which they communicate ideas; and the future to which they are building towards. She notes “if the curriculum we use to teach our children does not connect in positive ways to the culture that young people bring to school or prepare them for the future they are building towards, it is doomed for failure”
Delpit (2012) points out that part of the struggle with standardized curriculums (the curriculum that is taught in schools today) is that it does not completely address the individual child: the culture from which they come; the language in which they communicate ideas; and the future to which they are building towards. She notes “if the curriculum we use to teach our children does not connect in positive ways to the culture that young people bring to school or prepare them for the future they are building towards, it is doomed for failure”
References:
Barr, C., Doyle, M., Clifford, J., De Leo,T., Dubeau, C. (2003). "There is More to Math: A Framework for Learning and Math Instruction” Waterloo Catholic District School Board
Delpit, L. D. (2012). "Multiplication is for white people”: Raising expectations for other people's children. New York: NEW Press Rittle-Johnson, B., & Alibali, M. W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology, 91(1), 175-189. Wolfram, C. (2010). Conrad Wolfram: Teaching kids real math with computers. [Video file]. Retrieved from: http://www.ted.com/talks/conrad_wolfram_teaching_kids_real_math_with_computers.html Star, J. R. (2002). Re-conceptualizing procedural knowledge: The emergence of “intelligent” performances among equation solvers. In D. Mewborn, P. Sztajn, D. White, H. Wiegel, R. Bryant, & K. Nooney (Eds.), Proceedings of the 28th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 999-1007). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. |
Conrad Wolfram (Ted Summit 2010). For more information check out
<http://www.ted.com/talks/conrad_wolfram_teaching_kids_real_math_with_computers.html> |
